Beal's conjecture
Beal's conjecture is a conjecture in number theory proposed by Andrew Beal in about 1993; a similar conjecture was suggested independently at about the same time by Andrew Granville.
While investigating generalizations of Fermat's last theorem in 1993, Beal formulated the following conjecture:
If
where A, B, C, x, y, and z are positive integers with x, y, z > 2 then A, B, and C must have a common prime factor.
Beal has offered a prize of US$100,000 for a proof of his conjecture or a counterexample[1].
Contents |
Examples
To illustrate, the solution 33 + 63 = 35 has bases with a common factor of 3, and the solution 76 + 77 = 983 has bases with a common factor of 7. Indeed the equation has infinitely many solutions, including for example
for any  ,
,  ,
, 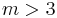 . But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor
. But no such solution of the equation is a counterexample to the conjecture, since the bases all have the factor 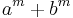 in common.
in common.
The example 73 + 132 = 29 shows that the conjecture is false if one of the exponents is allowed to be 2.
Properties
By computerized searching, greatly accelerated by aid of modular arithmetic, this conjecture has been verified for all values of all six variables up to 1000.[2] So in any counterexample, at least one of the variables must be greater than 1000.
A variation of the conjecture where x, y, z (instead of A, B, C) must have a common prime factor is not true. See, for example 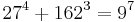 .
.
Beal's conjecture is a generalization of Fermat's last theorem, which corresponds to the case 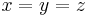 . If
. If 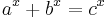 with
with 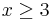 , then either the bases are coprime or share a common factor. If they share a common factor, it can be divided out of each to yield an equation with smaller, coprime bases.
, then either the bases are coprime or share a common factor. If they share a common factor, it can be divided out of each to yield an equation with smaller, coprime bases.
The conjecture is not valid over the larger domain of Gaussian integers. After a prize of $50 was offered for a counterexample, Fred W. Helenius provided (−2 + i)3 + (−2 − i)3 = (1 + i)4.[3]
References
External links
- http://www.bealconjecture.com/
- http://www.math.unt.edu/~mauldin/beal.html
- R. Daniel Mauldin (1997). "A Generalization of Fermat’s Last Theorem: The Beal Conjecture and Prize Problem". Notices of the AMS 44 (11): 1436–1439. http://www.ams.org/notices/199711/beal.pdf.
- Beal's Conjecture at PlanetMath.
- http://mathoverflow.net/questions/28764/status-of-beal-tijdeman-zagier-conjecture
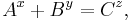
![\left[a \left(a^m %2B b^m\right)\right]^m %2B \left[b \left(a^m %2B b^m\right)\right]^m = \left(a^m%2Bb^m\right)^{m%2B1}](/2012-wikipedia_en_all_nopic_01_2012/I/a04866e6b07e69158801f5f43762dc36.png)